عملگرهای بیتی و تکنیک های پر کاربرد با آنها

همه ما از عملگرهای ریاضی یا منطقی بطور معمول استفاده میکنیم، اما گاهی بسیار راحت تر و خیلی اوقات بسیار بهینه تر است اگر از عملگرهای بیتی استفاده کنیم.

دانستن تکنیک های بیتی در مهندسی معکوس  بسیار کارا است. زیرا خیلی از optimization های انجام شده توسط کامپایلر از عملیات های بیتی بهره میبرند.

عملگرهای بیتی همانطور که از نام آنها پیداست در سطح بیت عملیات انجام داده و کنترل انجام عملیات در این سطح را در اختیار ما می گذراند.

در این پست در مورد 6 عملگر بیتی معمول خواهیم گفت:

عملگرهای بیتی

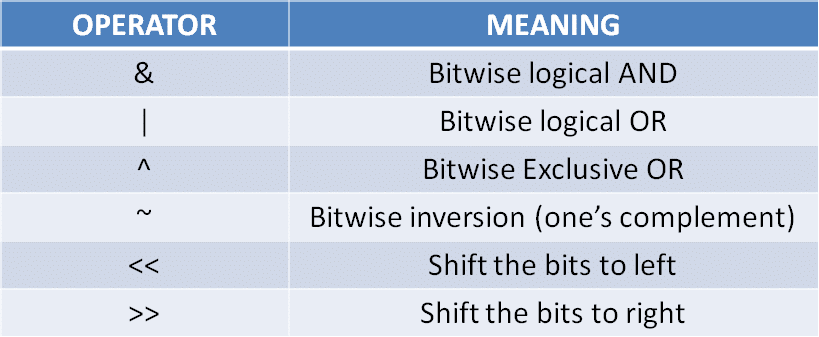
1 2 3 4 5 6

AND              : & OR               : | XOR              : ^ NOT (COMPLEMENT) : ~ SHIFT (RIGHT)    : << SHIFT (LEFT)     : >>

در این بین عملگرهای AND و OR و XOR جبری دوطرفه هستند. یعنی دو ورودی گرفته و یک خروجی میدهند و فرقی اگر سمت چپ و راست ورودی را با هم جابجا کنیم جواب یکسان خواهد بود. درست مانند عملگر ریاضی SUM یا + یا همان جمع.

1 2	>> 2 = 00001100 00110000 >> 3 =

عملگر NOT و یا همان  COMPLEMENT تنها یک ورودی میگیرد و یک خروجی میدهد.

عملگرهای SHIFT دو ورودی گرفته اما جبری نیستند. یعنی مقادیر سمت چپ و راست با هم جابجا شوند جواب تغییر خواهد کرد.

نکته: این عملگرها بیتی هستند. یعنی اصولا بر روی بیت ها کار میکنند. اندازه مقادیر در چهار عملگر اول گفته شده تأثیری ندارد از آنجایی که در اصل عملکرد آنها برروی یک عدد مانند لیست کردن بیت های دو مقادیر و انجام آن عملیات ها بر روی هر بیت در این دو لیست است. در ادامه مثال ها را خواهید دید.

عملگرها و نحوه عملکرد آنها

عملگر AND

درست مانند معنی لغوی AND, یعنی ‘و’, بدین معنی است که هر دو طرف باید ۱ باشند.

1 2 3 4

1 & 1 = 1 1 & 0 = 0 0 & 1 = 0 0 & 0 =0

از این عملگر در  MASK  کردن بسیار استفاده میشود. بعنوان مثال وقتی شما تنها ۳ بیت آخر را میخواهید, میتوانید از این تکنیک استفاده کنید:

1	1010011 & 111 = 11

مقدار مورد نظر را با عددی که تنها بیت های مورد نظر آن تنظیم است AND کنید و خروجی بیت های عدد خروجی طوری خواهد بود که اگر بیت های عدد اول در بیت های ۱ عدد دوم ۱ بودند در خروجی باقی خواهند ماند. از این نکته در تکنیک های Bit Flags و پیدا کردن باقیمانده نیز استفاده میشود.

نکته: AND هر عدد با صفر, صفر خواهد بود.

عملگر OR

خروجی این عملگر در صورتی ۱ خواهد بود که هر دو یا یکی از طرفین ۱ باشند.

1 2 3 4

1 | 1 = 1 1 | 0 = 1 0 | 1 = 1 0 | 0 = 0

با استفاده از این عملگر میتوانید بیت های یک عدد را ۱ کرده و دیگر بیت ها را به حالت اولیه خود باقی بگذارید, تنظیم سه بیت آخر:

1	100100 | 000111 = 100111

نکته: OR هر عدد با صفر همان عدد خواهد بود.

 عملگر XOR

از جالب ترین عملگرهای بیتی است و تکنیک های سطح بالای بسیار حیاتی ای با استفاده از آن انجام شده است.

خروجی این عملگر در صورتی یک خواهد بود که تنها یکی از طرفین ۱ باشد.

1 2 3 4

1 ^ 1 = 0 1 ^ 0 = 1 0 ^ 1 = 1 0 ^ 0 = 0

عملگر XOR مخفف eXclusive OR میباشد و در خروجی تفاوت بیتی بین دو مقدار را نشان میدهد.

با داشتن این تفاوت و یکی از طرفین میتوان طرف دیگر را بدست آورد.

1 2 3 4 5 6 7 8

12 ^ 16 = 28 12 ^ 14 = 2   12 ^ 28 = 16 12 ^ 2  = 14   16 ^ 28 = 12 14 ^ 2  = 12

از این تکنیک برای رمزنگاری symmetric به همین نام XOR استفاده شده است.

همینطور از این تکنیک برای کم کردن Redundancy اطلاعات backup در برخی نسخه هایتکنولوژی RAID نیز استفاده شده است.

برای محاسبه  Hamming Distance نیز استفاده میشود که کاربرد فراوانی در تست صحت اطلاعات, اندازه گیری نویز و نهایتا یادگیری ماشینی دارد.

نکته: xor دو عدد یکسان با یکدیگر صفر است. زیرا هیچ تفاوتی ندارند.

عملگر NOT و یا COMPLEMENT

این عملگر هر بیت دریافت شده را معکوس میکند:

1 2 3 4 5

~ 1 = 0 ~ 0 = 1   ~ 110011 = 001100 ~ 100000 = 011111

عملگر SHIFT RIGHT

این عملگر دو عملوند میگیرد:

1. عملوند مقدار که عملیات shift بر روی آن انجام میشود. عملوند سمت راست این نقش را ایفا میکند.
2. عملوند تعداد که عمل shift با استفاده از آن بر روی عملوند ۱ انجام میشود. عملوند سمت راست این نقش را ایفا میکند.

عملگر shift به سمت راست به تعداد عملوند ۲ به سمت چپ عملوند ۱ بیت های ۰ اضافه کرده و به همان تعداد نیز بیت های سمت راست را بر میدارد.

اگر لیست بیت ها را یک بسته لوله ای از توپ ها که دو طرف آن باز است در نظر بگیریم و بیت های ۱ توپ رنگ سبز و بیت های ۰ توپ رنگ سفید باشند. shift به سمت راست به n تعداد مانند این است که از سمت چپ n تعداد توپ سفید هل دهیم. اینکار باعث میشود n تعداد توپ های سمت راست که داخل بسته لوله ای بوده اند از سمت راست به بیرون هل داده شده و خارج شوند.

1 2 3

00110000 >> 2 = 00001100 00110000 >> 3 = 00000110 00110000 >> 4 = 00000011

عملگر SHIFT LEFT

این عملگر دقیقا مانند عملگر SHIFT RIGHT است اما برخلاف shift به راست, از سمت چپ بیت ها را بر میدارد و به سمت راست بیت های صفر اضافه می کند.

1 2 3

00001100 >> 2 = 00110000 00001100 >> 3 = 01100000 00001100 >> 4 = 11000000

تکنیک های بیتی

تکنیک پرچم ها یا همان Flags

به هر مقداری میتوان بعنوان یک عدد و یا لیستی از اعداد نگاه کرد و به هر عددی نیز میتوان بعنوان لیستی از بیت ها نگاه کرد. این دید این اجازه را به ما میدهد تا کنترل روی بیت ها را راحتتر درک کنیم.

فرض کنید میخواهید از یک لیستی از مقادیر منطقی یا همان boolean استفاده کنید که هر خانه در این لیست مفهوم ثابتی دارد. بعنوان مثال ساختار دسترسی به فایل در لینوکس را در نظر بگیرید:

1 2 3 4 5 6 7 8

permission = {READ, WRITE, EXEC} R = 0 W = 1 X = 2   has_read_access = permission[R] has_write_access = permission[W] has_exec_access = permission[X]

حال به یک عدد بعنوان لیست از بیت ها نگاه کنید. آیا میتوان همین سیستم را با اعداد و عملگر های بیتی پیاده سازی کرد؟

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

permission = RWX R = 1 << 2 = 100 W = 1 << 1 = 010 X = 1 << 0 = 001   // get corresponding bit has_read_access = permission & R has_write_access = permission & W has_exec_permission = permission & X   /// set corresponding bit   // set read access permission = permission | R // set write access permission = permission | W // set exec access permission = permission | X   /// unset corresponding bit   // unset read access permission = permission & ~(R) // unset write access permission = permission & ~(W) // unset exec access permission = permission & ~(X)

تکنیک تبدیل حرف کاراکتر ASCII به حرف بزرگ

نکته: این تکنیک تنها بر روی حروف A-Z و a-z کاربرد دارد. استفاده از این تکنیک برای دیگر کاراکترها ممکن است پیامد منفی داشته باشد.

نکته: در این تکنیک فرقی نمیکند کاراکتر حرف بزرگ باشد یا کوچک. خروجی یکسان خواهد بود.

1 2 3 4 5 6 7 8 9 10

'A' = 1(0)00001 'Z' = 1(0)11010 'a' = 1(1)00001 'z' = 1(1)11010 '_' = 1(0)11111   'A' & '_' = 'A' 'Z' & '_' = 'Z' 'a' & '_' = 'A' 'z' & '_' = 'Z'

تکنیک تبدیل حرف کاراکتر ASCII به حرف کوچک

نکته: این تکنیک تنها بر روی حروف A-Z و a-z کاربرد دارد. استفاده از این تکنیک برای دیگر کاراکترها ممکن است پیامد منفی داشته باشد.

نکته: در این تکنیک فرقی نمیکند کاراکتر حرف بزرگ باشد یا کوچک. خروجی یکسان خواهد بود.

1 2 3 4 5 6 7 8 9 10

'A' = 1(0)00001 'Z' = 1(0)11010 'a' = 1(1)00001 'z' = 1(1)11010 ' ' = 0(1)00000   'A' | ' ' = 'a' 'Z' | ' ' = 'z' 'a' | ' ' = 'a' 'z' | ' ' = 'z'

تکنیک به n توان رساندن ۲

هر بیت در یک عدد نگهدارنده ی ۲ بتوان اندیس آن بیت در آن عدد است. این نکته به وفور در تبدیل مبنا استفاده میشود.

در این قسمت از این نکته برای تسریع محاسبه استفاده می کنیم:

1 2 3 4 5 6 7 8 9

pow(2, n) = 1 << n   pow(2, 0) = 1 << 0 =  1 pow(2, 1) = 1 << 1 =  2 pow(2, 2) = 1 << 2 =  4 pow(2, 3) = 1 << 3 =  8 pow(2, 4) = 1 << 4 = 16 pow(2, 5) = 1 << 5 = 32 ...

تکنیک ضرب x در ۲ به توان n

در اعداد مبنای ۱۰ داریم که ضرب هر عدد در عددی مانند ۱۰ که یک رقم ۱ در اول و مابقی ارقام ۰ دارد برابر است با همان عدد اما اضافه شدن صفر های عدد ضریب به انتهای عدد. مانند:

1 2	123 * 10 = 1230 123 * 1000 = 123000

اعداد مبنای ۲ از این قاعده مستثنا نیستند و در مبنای دو نیز میتوانید همینکار را انجام دهید. اما نکته قابل توجه اینجا است که:

1 2	1 << 3 = 8 1 << 4 = 16

بنابراین:

1 2	3 << 2 = 3 * pow(2, 2) = 3 * 4 = 12 3 << 3 = 3 * pow(2, 3) = 3 * 8 = 24

تکنیک تقسیم x بر ۲ به توان n

درست مانند ضرب اما بجای استفاده از shift به سمت چپ از shift به سمت راست استفاده می کنیم تا از بیت های سمت راست کاسته شود:

1 2	12 >> 2 = 12 / pow(2, 2) = 12 / 4 = 3 24 >> 3 = 24 / pow(2, 3) = 24 / 8 = 3

تکنیک باقیمانده تقسیم x بر ۲ به توان n

در تکنیک تقسیم x بر ۲ به توان n گفته شد که “از shift به سمت راست استفاده میکنیم تا از بیت های سمت راست کاسته شود”. بیت های کاسته همان باقی مانده ها هستند. برای نگه داری این باقیمانده از این تکنیک استفاده می کنیم:

1 2 3 4 5 6

1 >> 3       = 1000 = 8 (1 >> 3) - 1 = 0111 = 7   x & ((1 >> n) - 1) = remainder   22 & ((1 >> 3) - 1) = 22 & 7 = 10110 & 00111 = 00110 = 6