جمع و ضرب چند جمله ای ها در پایتون

چند جمله ای ها در پایتون

اگر برنامه نویس باشید به طبع در حین برنامه نویسی توابع و اشکال مختلف اعمال ریاضی را در بدنه کد خود بکار برده اید. امروز می خواهیم نحوه پیاده سازی چند جمله ای ها در پایتون را به شما آموزش دهیم. نکته مهمی که در خصوص اجرای کدهای توابع ریاضی در برنامه نویسی وجود دارد، پیچدگی زمانی آنها است. در صورت استفاده از توابع چند جمله ای در پایتون هر چه درجه چند جمله ای بیشتر باشد تعداد ضرب های داخل کد نیز به صورت نمایی افزایش می یابد. حال چرا پیچدگی زمانی برای کد بسیار مهم است؟

پیچدگی زمانی با بهینه بودن کد

امروزه اگر در حوزه برنامه نویسی مشغول فعالیت باشید می دانید که همواره یکی از چالش های سر راه شما بهینه بودن کد است. راه های مختلفی برای رسیدن به حداکثر بهینگی وجود دارد اما اگر در بدنه کد خود توابع ریاضی و چند جمله داشته باشید چگونه کد خود را بهینه می کنید؟ آیا صرف بهینه بودن اجرا کافی است؟ اگر جواب شما مثبت است به این فکر کنید که چرا مهندسین نرم افزار مفهوم پیچدگی زمانی را برای الگوریتم ها تعریف کردند؟

هر برنامه نویسی که در حال کد زدن و ساخت انواع مختلف نرم افزار ها است میداند که بایستی نرم افزار نهایی که تولید میشود در نهایت بهینگی و دارای بیشترین سرعت عمل باشد، چرا که اصل مهم این است که نرم افزار در سیستم کاربر نهایی به راحتی و بدون هیچ مشکلی و با سریعترین زمان ممکن اجرا شود. پس همیشه باید در نظر داشته باشد کاربر نهایی ممکن است از نظر منابع سیستمی در حدقل شرایط ممکن قرار داشته باشد و باید کد به گونه ای بهینه باشد که حتی در صورت وجود محدودیت منابع به درستی و در سریع ترین زمان ممکن اجرا شود.

نحوه تعریف توابع چند جمله ای در پایتون

اگر برنامه نویس زبان پایتون باشید حتما کتابخانه های معروف مربوط به علوم ریاضی مانند numpy و math را می شناسید. در این پست با استفاده از این کتابخانه ها نحوه تعریف چند جمله ای ها در پایتون و سپس جمع و ضرب آنها را به شما آموزش می دهیم.

توابع چند جمله ای چیست و چگونه در متن برنامه این توابع را تعریف کنیم؟

تابع یک جمله ای: ابتدا بهتر است با مفهوم تابع یک جمله‌ ای آشنا شوید. این تابع بر حسب متغیر x به صورت a x^n نمایش داده می‌شود. در این عبارت یک جمله ای a یک عدد حقیقی است که ضریب نام دارد. n یک عدد حسابی است (شامل صفر و اعداد طبیعی) که اگر n صفر باشد چون توان صفر برابر یک است، یعنی جمله ما فقط از یک عدد تشکیل می‌شود. پس نتیجه می‌گیریم اعداد نیز جزء یک جمله‌ ای‌ ها هستند.

تابع چند جمله ای: این تابع از مجموع چند تابع یک جمله‌ ای تشکیل می‌شود. پس در اینجا نیز توان متغیر فقط عدد حسابی می‌تواند باشد.

تابع توانی: تابعی با یک جمله واحد است که حاصل‌ضرب یک عدد حقیقی و یک متغیر است که به یک توان یک عدد حقیقی ثابت رسیده است (عددی که در متغیر ضرب می‌شود، به عنوان ضریب شناخته می‌شود). به عنوان یک مثال، تابع مساحت یا حجم را در نظر بگیرید. تابع مساحت یک دایره با شعاع r برابر است با:

A(r)=πr^2

و تابع حجم یک کره با شعاع r نیز به شکل زیر است:

V(r)=4/3πr^3

هر یک از این مثال‌ها یک تابع توانی است، زیرا از ضرب یک π یا 4/3π در متغیر r به توان یک عدد حقیقی تشکیل شده است. ما فقط با چند جمله ای در یک متغییر x سر و کار خواهیم داشت. شکل کلی یک چند جمله ای در یک متغییر به شکل زیر است:

تابع چند جمله ای

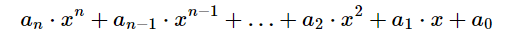
در مثال بالا an ضرایب ثابت بوده (اعداد صحیح غیر منفی) و x نامعین یا متغییر است. اصطلاح “نامعین” به این معنی است که هیچ ارزش خاصی را نشان نمی دهد، اما هر مقدار ممکن است جایگزین آن شود.این عبارت معمولا با عملگر جمع نوشته می شود:

خلاصه شده تابع چند جمله ای

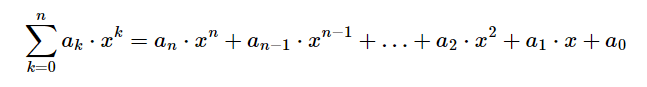
تابع چند جمله ای تابعی است که می توان آن را با ارزیابی یک چند جمله ای تعریف کرد. تابع f از یک آرگومان را می توان به صورت زیر تعریف کرد:

شکل کلی تابع

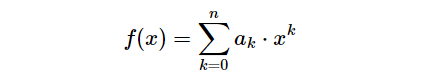
حال در محیط پایتون این توابع را پیاده سازی می کنیم:

#Define function for calculate the value of polynomial in X
def poly(A, x):
    p = A[-1]
    i = len(A) - 2
    while i >= 0:
        p = p * x + A[i]
        i -= 1
    return p

# enter your polynomial as : C + A x^1 + B x^2 + ..... + Z x^n
A = [1,2,3]

# enter X as intiger
x = 3

# priting result
print("Value of polynomial is :" , poly(A, x))

output:
Value of polynomial is : 34

نحوه تعریف تابع چند جمله ای را مشاهده کردید. ممکن است همیشه توابع ریاضی در بدنه کد بکار برده نشوند اما بایستی نحوه تعریف این نوع تابع ها را نیز بدانید چرا که در بعضی شرایط و برنامه نویسی ها فرمول های فیزیک و شیمی برای انجام انواع نختلف محاسبات نیاز به تعریف توابع چند جمله ای دارند. نکته بسیار مهم در این قسمت توان تابع مورد استفاده است. همان طور که پیش تر توضیح داده شد با افزایش توان چند جمله ای ها، پیچیدگی زمانی اجرای الگوریتم ما نیز افزایش می یابد. برای حل این مشکل از روش دانشمند قرن 19 به نام هورنر استفاده می کنیم.

روش هورنر برای حل توابع چند جمله ای

در ریاضیات روش هورنر الگوریتمی برای ارزیابی چند جمله ای است. اگرچه این روش به نام ویلیام جورج هورنر نامگذاری شده است، اما بسیار قدیمی تر است، زیرا توسط خود هورنر به جوزف-لوئیس لاگرانژ نسبت داده شده است و می توان آن را به صدها سال پیش در ریاضیدانان چینی و ایرانی ردیابی کرد.

پس از معرفی کامپیوترها، این الگوریتم برای محاسبات کارآمد با چند جمله ای ها اساسی شد. الگوریتم بر اساس قانون هورنر است:

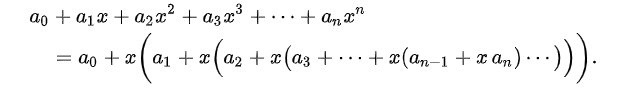
این امکان ارزیابی یک چند جمله‌ای درجه n را تنها با n ضرب و n جمع می‌دهد، زیرا چند جمله‌ای درجه n وجود دارد که با عملیات‌های حسابی کمتری قابل ارزیابی نیستند. روش هورنر همچنین به روشی برای تقریب ریشه‌های چندجمله‌ای اشاره دارد.

می توان برای ارزیابی چند جمله ای در زمان O(n) استفاده کرد. برای درک روش، اجازه دهید مثال 2×3 – 6×2 + 2x – 1 را در نظر بگیریم. بر اساس روش هورنر چند جمله ای را می توان به صورت ((2x – 6)x + 2)x – 1 ارزیابی کرد.

ایده این است که نتیجه را به عنوان ضریب xn که در این مورد 2 است، مقداردهی اولیه کنیم، بارها نتیجه را در x ضرب کنیم و ضریب بعدی را به نتیجه اضافه کنیم. در نهایت نتیجه را چاپ میکنیم.

# returns value of poly[0]x(n-1)+ poly[1]x(n-2) + .. + poly[n-1]
def horner(poly, n, x):
    result = poly[0]

    # Evaluate value of polynomial using Horner
    for i in range(1, n):
        result = result*x + poly[i]
    return result

# enter your polynomial as : Z x^n + ....+ B x^2 + A x^1 + C
poly = [3,2,1]

# enter X as intiger
x = 3

n = len(poly)

#print the value of polynomial in X
print("Value of polynomial is " , horner(poly, n, x))

output : 
Value of polynomial is : 34

مشاهده کردید که به راحتی میتوان با استفاده از روش هورنر پیچیدگی زمانی اجرای الگوریتم ها را بسیار کوتاه کرد. شاید در عمل و برنامه های کوچک و توان کوچک نتوان تاثیر این روش را زیاد درک کرد اما در محیط برنامه های چند هزار خطی قطعا این روش زمان اجرای برنامه را کوتاه تر میکند.

جمع دو تابع چند جمله ای در پایتون

حال برای جمع چند جمله ای ها در پایتون، ابتدا بایستی نحوه جمع دو تابع در علم ریاضی را بدانیم. با توجه به دو چند جمله ای که با دو آرایه نشان داده شده اند، تابعی می نویسیم که دو چند جمله ای داده شده را جمع کند.

def add(P, Q, m, n):
    size = max(m, n)
    sum = [0 for i in range(size)]

    # Initialize the polynomial  
    for i in range(0, m, 1):
        sum[i] = P[i]

    # Take ever term of first polynomial
    for i in range(n):
        sum[i] += Q[i]
    return sum

# A utility function to print a polynomial
def printPoly(poly, n):
    for i in range(n):
        print(poly[i], end = "")
        if (i != 0):
            print("x^", i, end = "")
        if (i != n - 1):
            print(" + ", end = "")

if __name__ == '__main__':
    
    # enter your polynomial as : C + A x^1 + B x^2 + ..... + Z x^n
    P = [5, 0, 10, 6, 4]

    # enter your polynomial as : C + A x^1 + B x^2 + ..... + Z x^n
    Q = [1, 2, 4]

    # m and n are sizes of P[] and Q[] respectively
    m = len(P)
    n = len(Q)
    sum = add(P, Q, m, n)
    size = max(m, n)

    # print results ;
    print("First polynomial is : ")
    printPoly(P, m)
    print("\n", end = "")
    print("Second polynomial is : ")
    printPoly(Q, n)
    print("\n", end = "")
    print("sum polynomial is : ")
    printPoly(sum, size)

خروجی:

First polynomial is :
5 + 0x^1 + 10x^2 + 6x^3
Second polynomial is :
1 + 2x^1 + 4x^2
Sum polynomial is :
6 + 2x^1 + 14x^2 + 6x^3

پیچیدگی زمانی الگوریتم و برنامه فوق O(m+n) است که در آن m و n مرتبه های دو چند جمله ای معین هستند.

ضرب دو تابع چند جمله ای در پایتون

حال برای ضرب دو تابع چند جمله ای نیز داریم، در این قسمت یک برنامه با استفاده از NumPy برای ضرب یک چند جمله ای در دیگری می سازیم. دو چند جمله ای به عنوان ورودی داده می شود و حاصل ضرب دو چند جمله ای است.

چند جمله ای p(x) = C3 x2 + C2 x + C1 در NumPy به صورت : ( C1, C2, C3 ) { ضرایب (ثابت)} نشان داده می شود.
اجازه دهید دو چند جمله‌ای p(x) و q(x) را در نظر بگیریم، سپس آنها را ضرب کنیم تا r(x) = p(x) * q(x) در نتیجه ضرب دو چند جمله‌ای ورودی به دست آید.

اگر دو چند جمله ای به صورت زیر باشند:

p(x) = A3 x2 + A2 x + A1
q(x) = B3 x2 + B2 x + B1

حاصل ضرب آنها به صورت زیر خواهد بود:

r(x) = p(x) * q(x)

در خروجی به شکل زیر نشان داده میشود:

((A1 * B1) ,(A2 * B1)+(A2 * B1),(A3 * B1)+(A2 * B2)+(A1 * B3) ,(A2 * B2)+(A3 * B2), (A3 * B3)).

این را می توان با استفاده از روش polymul در NumPy محاسبه کرد. این روش حاصل ضرب دو چند جمله‌ای را ارزیابی می‌کند و چند جمله‌ای حاصل از ضرب دو چند جمله‌ای ورودی «p1» و «p2» را برمی‌گرداند.

#import packages
import numpy
from numpy.polynomial import Polynomial

# enter your polynomial as : C + A x^1 + B x^2 + ..... + Z x^n
px = (-7,6,-2,2,0,1)

# enter your polynomial as : C + A x^1 + B x^2 + ..... + Z x^n
qx = (2,6,0,0,5)

# multiplication the polynomials
rx = numpy.polynomial.polynomial.polymul(px, qx)

# result r(x) = p(x) * q(x)
# output is ( (A1 * B1), (A2 * B1) + (A2 * B1),(A3 * B1) + (A2 * B2) + (A1 * B3), (A2 * B2) + (A3 * B2), (A3 * B3) ).
# print the result

print(Polynomial(rx))
print (rx)
output :

-14.0 - 30.0 x**1 + 32.0 x**2 - 8.0 x**3 - 23.0 x**4 + 32.0 x**5 -4.0 x**6 + 10.0 x**7 + 0.0 x**8 + 5.0 x**9

[-14. -30.  32.  -8. -23.  32.  -4.  10.   0.   5.]

تقسیم توابع چند جمله ای در پایتون

روش تقسیم هورنر ابزار کارآمدی برای محاسبه چنین ضرایب و باقیمانده‌ها فراهم می‌کند. با توجه به چند جمله‌ای f(x) و g(x) در x نامشخص، چند جمله‌ای (ضریب) و r(x) (باقیمانده) را به‌گونه‌ای محاسبه می‌کنیم که f(x)=g(x)q(x)+r(x) که در آن r(x)=0 یا درجه r(x) کوچکتر از درجه g(x) است.

میخواهیم تابع f(x) را به g(x) تقسیم کنیم:

f(x)= 3*x^5 - 8*x^4 - 5*x^3 + 26*x^2 - 33*x + 26
g(x)= x^3 - 2*x^2 - 4*x + 8

ورودی های جدول زیر با استفاده از روش هورنر محاسبه می شوند. ردیف پایین لیستی از ضرایب و باقیمانده هنگام تقسیم f(x) بر g(x) است. ضرایب به رنگ قرمز و باقیمانده به رنگ آبی هستند.

تقسیم به روش هورنر

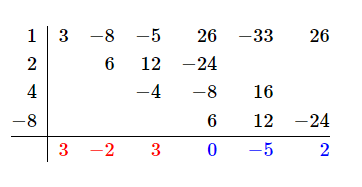
بنابراین:

f(x)= g(x)q(x)+r(x)
q(x)= 3x^2 - 2x + 3
r(x)= -5x + 2

ضرایب خارج قسمت به صورت زیر محاسبه می شود:

نحوه بدست آوردن ضرایب خارج قسمت

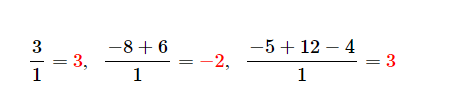
در اینجا تقسیم با محاسبه باقی مانده با کمی جزئیات بیشتر را مشاهده می کنید:

تقسیم چند جمله با جزییات ببشتر

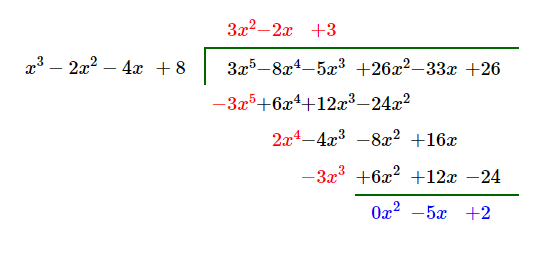
در شکل نوشته قرمز خارج قسمت و نوشته آبی باقی مانده تقسیم است.

در محیط پایتون نیز برای پیاده سازی داریم، اگر ورودی ها p(x) و g(x) به صورت زیر باشد:

p(x) = A3 x2 + A2 x + A1
g(x) = B3 x2 + B2 x + B1 

بنابراین خروجی به صورت زیر است:

q(x) = p(x) // g(x) and r(x) = p(x) % g(x)

در پایتون نیز به صورت زیر می باشد:

import numpy
from numpy.polynomial import Polynomial

# define the polynomials as : C + A x^1 + B x^2 + ..... + Z x^n
px = []
gx = []

# divide the polynomials
qx , rx = numpy.polynomial.polynomial.polydiv(px, gx)

# print the result

# quotient
print('quotient is :',Polynomial(qx))

# remainder
print('reminder is :' , Polynomial(rx))

خروجی :

quotient is : c + a x**1 + ....

reminder is : c + a x**1 + ...